by Dominik Fuchsgruber, Tom Wollschläger, Johannes Bordne, Stephan Günnemann

Published at the Forty-Second International Conference on Machine Learning (ICML), 2025.

Abstract

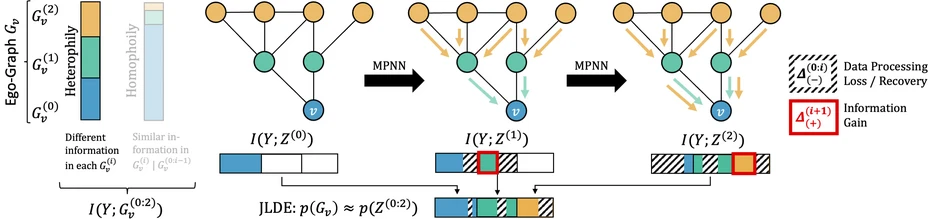
While uncertainty estimation for graphs recently gained traction, most methods rely on homophily and deteriorate in heterophilic settings. We address this by analyzing message passing neural networks from an information-theoretic perspective and developing a suitable analog to data processing inequality to quantify information throughout the model's layers. In contrast to non-graph domains, information about the node-level prediction target can increase with model depth if a node's features are semantically different from its neighbors. Therefore, on heterophilic graphs, the latent embeddings of an MPNN each provide different information about the data distribution -- different from homophilic settings. This reveals that considering all node representations simultaneously is a key design principle for epistemic uncertainty estimation on graphs beyond homophily. We empirically confirm this with a simple post-hoc density estimator on the joint node embedding space that provides state-of-the-art uncertainty on heterophilic graphs. At the same time, it matches prior work on homophilic graphs without explicitly exploiting homophily through post-processing.

Cite

Please cite our paper if you use the model, experimental results, or our code in your own work:

t.b.d.

Links

t.b.d.