Background
Over the last decade, interactive, yet physics-based dynamic simulation of deformable volumetric objects has received increasing attention. Applications range from surgery simulation, medical imaging and solid mechanics to computer animation and virtual sculpting. In these scenarios, physical correctness is often sacrificed for efficiency, resulting in approximate behavioural simulations or in the restriction to non-realistic material properties and small deformations.
CPU Multigrid Solver
In this research project, we overcome many of the limitations of previous methods by developing a generic real-time multigrid framework for constructing interactive and stable solvers for the governing equations of motion of deformable volumetric objects. This framework is open to a variety of different formulations of strain, i.e. linear, corotational and non-linear. By taking advantage of a finite element hierarchy, the proposed solvers are significantly faster than previous solution methods. Due to the linear asymptotic complexity of the multigrid solvers, with increasing problem size an ever increasing performance gain compared to previous approaches is achieved.
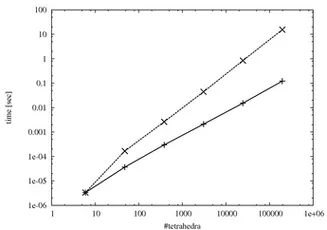
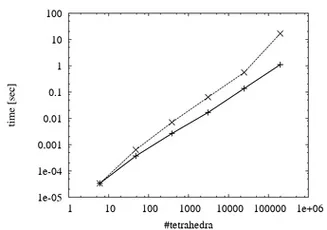
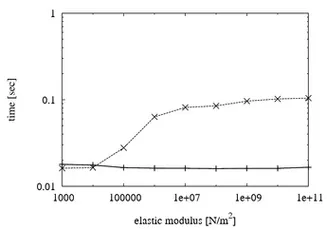
Compared to the standard preconditioned conjugate gradient method (dashed line) the run-time behavior of the multigrid solver (solid line) becomes increasingly better for large models (left) and stiffer materials (right)
(Timings were measured on a Intel Core 2 6600 2.4GHz processor using a single simulation thread)
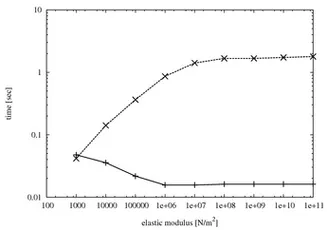
The multigrid solver (solid line) can even outperform the preconditioned conjugate gradient method (dashed line) in the case of corotatational finite elements. Then, the system matrix and the multigrid solver have to be rebuilt in every simulation step. The performance gain becomes increasingly better for large models (left) and stiffer materials (right)
(Timings were measured on a Intel Core 2 Duo 6600 2.4GHz processor using a simulation thread and a matrix reassembling thread)


Animations (click to get movies)
GPU Collision Detection
We have integrated an algorithm for collision detection within the simulation framework. The design goal of this algorithm was to take the scene geometry as it is represented on the GPU for rendering purpose. In particular, this make the method amenable to the handling of geometry that is arbitrarily modified or created on the GPU. Usually, a high resolution mesh rather than the simulation mesh is used to render the deformed object. However, if collision detection is performed on the simulation mesh only, rendering artifacts can occur. Using our algorithm, collision detection can be performed directly on the render mesh. Only potentially colliding triangles have to be read back to the CPU to allow for exact intersection testing and collision response.
GPU Simulation
On a different avenue, we have developed and analyzed different implementations of mass-spring systems for interactive simulation of deformable objects on graphics processing units (GPUs). By exploiting features of recent graphics accelerators to simulate spring elongation and compression on the GPU, saving displaced point masses in graphics memory, and then sending these positions through the GPU again to render the deformed object, any CPU-GPU data transfer can be avoided at run-time. Because it is hard to control numerical stability of explicit mass-spring systems, the GPU implementation should only be considered in constraint applications using low resolution models. Then, the GPU system yields considerably better performance compared to the multigrid approach. On the other hand, the implicit multigrid framework enables much better control of material parameters and allows for an integration time step that is not dependent on material stiffness. Our experiments have also shown, that the implementation of an implicit mass-spring system as proposed by Baraff and Witkin on the GPU has several limitations. Neither is the GPU implementation reliable in terms of numerical accuracy nor is it more efficient than the CPU implicit multigrid approach. The reason therefore is twofold: First, limited numerical accuracy of the GPU conjugate gradient method introduces a significant error in the solution. Second, both the update of a random-sparse matrix and linear algebra operations on it can not be encoded efficiently on the GPU. In the future, we aim to extend the multigrid framework towards an implicit mass-spring system.
Publications
- A Hexahedral Multigrid Approach for Simulating Cuts in Deformable Objects
- A Real-Time Multigrid Finite Hexahedra Method for Elasticity Simulation using CUDA
- Interactive Deformations with Multigrid Skeletal Constraints
- A Streaming Approach for Sparse Matrix Products and its Application in Galerkin Multigrid Methods
- Stress Tensor Field Visualization for Implant Planning in Orthopedics
- A 3D Simulation System for Hip Joint Replacement Planning
- Corotated Finite Elements Made Fast and Stable
- Computational Steering for Patient-Specific Implant Planning in Orthopedics
- Interactive Simulation and Visualization in Joint Replacement Surgery
- Real-Time Simulation and Visualization of Deformable Objects
- Interactive Collision Detection for Deformable and GPU objects
- Freeform Image
- Interactive GPU-based Collision Detection
- Advanced Volume Rendering for Surgical Training Environments
- A Generic and Scalable Pipeline for GPU Tetrahedral Grid Rendering
- A Multigrid Framework for Real-Time Simulation of Deformable Bodies
- Interactive Simulation and Rendering of Heterogeneous Deformable Bodies
- A Multigrid Framework for Real-Time Simulation of Deformable Volumes
- Mass-Spring Systems on the GPU
- Interactive Simulation of Deformable Bodies on GPUs
- Physically Accurate Real-Time Simulation of Deformable Bodies for Surgical Training and Therapy Planning