Numerical Simulation on GPUs

Background

Real-time visual simulation still remains one of the key challenges in computer graphics applications. In this research project we develop GPU based techniques for this purpose. We target the GPU as a numerical coprocessor for a couple of reasons. First, aside from their current utility, GPUs present the first commercially successful examples of a class of future computing architectures key to high performance, cost effective super-computing. In particular, best performance is achieved if the ratio of numerical operations to memory accesses is large. Applications range from image processing and volume visualization to discrete transforms and numerical simulation. Second, as the simulation is carried out on the GPU, simulation results are already where they are needed for display - in local GPU memory. This eliminates CPU-GPU data transfer, which is likely to become the bottleneck otherwise.

Real-time computational fluid dynamics on the GPU (click for movies)

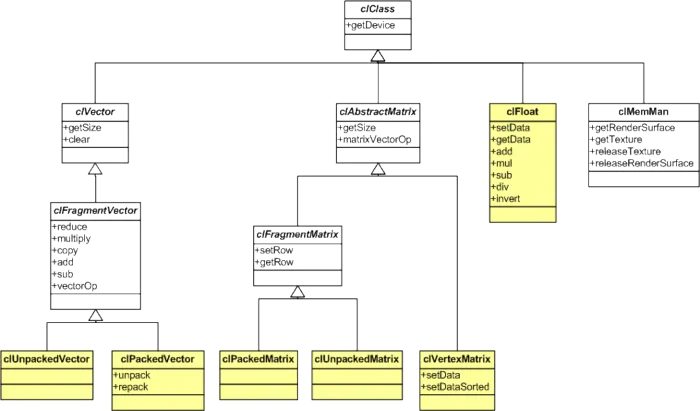
To be able to implement general techniques of numerical computing on the GPU, a GPU abstraction for this kind of application is required. Therefore we have developed a linear algebra framework. This framework allows the user to abstract from the underlying GPU data structures and algorithms, and to focus on the application itself rather than the GPU implementation.

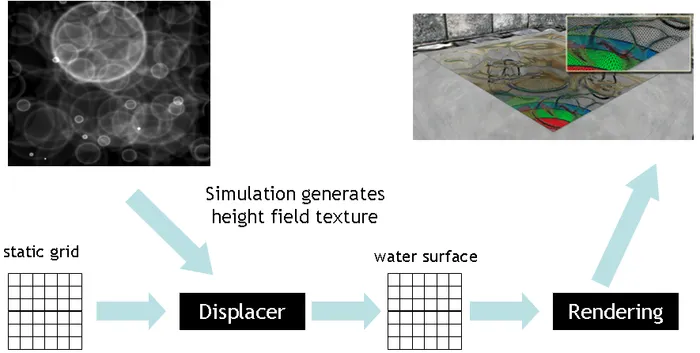
UML diagram of the LA framework (click to enlarge)

This framework facilitates the use of numerical simulation techniques to drive real-time visual effects. By using simulation results to advect geometric primitives on the GPU, saving displaced positions in graphics memory, and then sending these positions through the GPU again to obtain images in the frame buffer, a variety of different effects can be generated.

Simulation driven geometry modification (click to enlarge)

Real-time GPU-based modeling and rendering of hot gases, smoke and fire (click to enlarge)

In the future, 3D GPU-based simulation including complex obstacles and boundaries will be developed. In addition, new methods to employ numerical simulation techniques on the GPU for interactive shape modelling will be discovered.

This project is conducted in close collaboration with Peter Schröder at Caltech, and it is financially supported by the BaCaTeC initiative.

Numerical Simulation on GPUs

Background

Publications