Visualizing the Variability of Gradients in Uncertain 2D Scalar Fields
Tobias Pfaffelmoser, Mihaela Mihai, Rüdiger Westermann
Computer Graphics and Visualization Group, Technische Universität München, Germany
Background
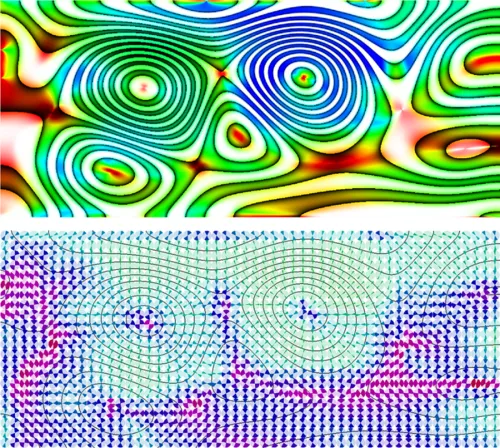
In uncertain scalar fields where data values vary with a certain probability, the strength of this variability indicates the confidence in the data. It does not, however, allow inferring on the effect of uncertainty on differential quantities such as the gradient, which depend on the variability of the rate of change of the data. Analyzing the variability of gradients is nonetheless more complicated, since, unlike scalars, gradients vary in both strength and direction. This requires initially the mathematical derivation of their respective value ranges, and then the development of effective analysis techniques for these ranges.
This paper takes a first step into this direction: Based on the stochastic modeling of uncertainty via multivariate random variables, we start by deriving uncertainty parameters, such as the mean and the covariance matrix, for gradients in uncertain discrete scalar fields. We do not make any assumption about the distribution of the random variables. Then, for the first time to our best knowledge, we develop a mathematical framework for computing confidence intervals for both the gradient orientation and the strength of the derivative in any prescribed direction, for instance, the mean gradient direction. While this framework generalizes to 3D uncertain scalar fields, we concentrate on the visualization of the resulting intervals in 2D fields. We propose a novel color diffusion scheme to visualize both the absolute variability of the derivative strength and its magnitude relative to the mean values. A special family of circular glyphs is introduced to convey the uncertainty in gradient orientation. For a number of synthetic and real-world data sets, we demonstrate the use of our approach for analyzing the stability of certain features in uncertain 2D scalar fields, with respect to both local derivatives and feature orientation.
A preprint of the article is available for download below. The definitive version is available at http://ieeexplore.ieee.org.
Associated Publications
Visualizing the Variability of Gradients in Uncertain 2D Scalar Fields
T. Pfaffelmoser, M. Mihai, R. Westermann, IEEE Transactions on Visualization and Computer Graphics, 2013 [Download] [Bibtex]