Generalization of Neural Combinatorial Solvers Through the Lens of Adversarial Robustness
Links
Abstract
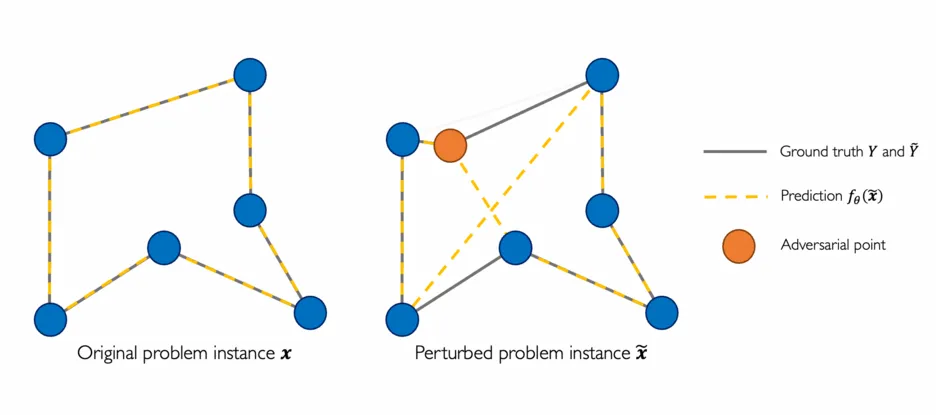
End-to-end (geometric) deep learning has seen first successes in approximating the solution of combinatorial optimization problems. However, generating data in the realm of NP-hard/-complete tasks brings practical and theoretical challenges, resulting in evaluation protocols that are too optimistic. Specifically, most datasets only capture a simpler subproblem and likely suffer from spurious features. We investigate these effects by studying adversarial robustness - a local generalization property - to reveal hard, model-specific instances and spurious features. For this purpose, we derive perturbation models for SAT and TSP. Unlike in other applications, where perturbation models are designed around subjective notions of imperceptibility, our perturbation models are efficient and sound, allowing us to determine the true label of perturbed samples without a solver. Surprisingly, with such perturbations, a sufficiently expressive neural solver does not suffer from the limitations of the accuracy-robustness trade-off common in supervised learning. Although such robust solvers exist, we show empirically that the assessed neural solvers do not generalize well w.r.t. small perturbations of the problem instance.
Cite
@inproceedings{geisler_rco2022,
title = {Generalization of Neural Combinatorial Solvers Through the Lens of Adversarial Robustness},
author = {Geisler, Simon and Sommer, Johanna and Schuchardt, Jan and Bojchevski, Aleksandar and G\"unnemann, Stephan},
booktitle={International Conference on Learning Representations (ICLR)},
year = {2022},
}