Stress Topology Analysis for Porous Infill Optimization

1 Chair for Computer Graphics and Visualization, Technical University of Munich, Germany

2 Department of Sustainable Design Engineering, Delft University of Technology, The Netherlands

Abstract

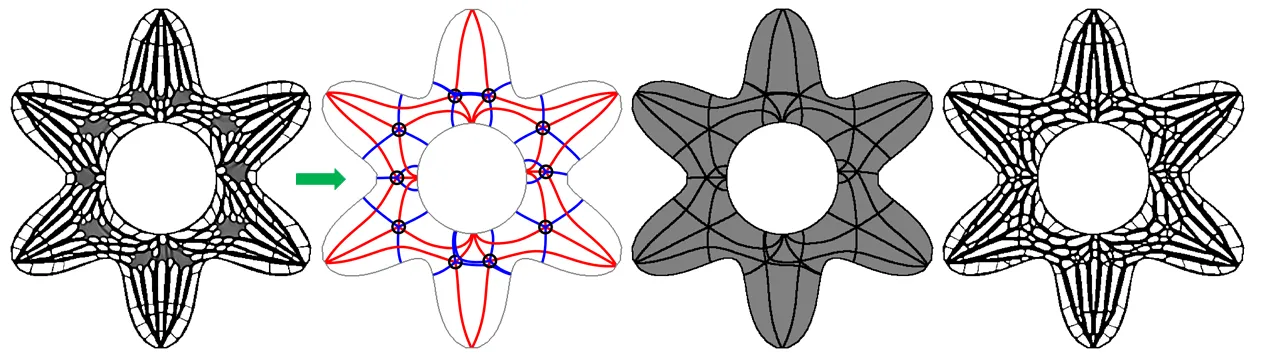
The optimization of porous infill structures via local volume constraints has become a popular approach in topology optimization. In some design settings, however, the iterative optimization process converges only slowly, or not at all even after several hundreds or thousands of iterations. This leads to regions in which a distinct binary design is difficult to achieve. Interpreting intermediate density values by applying a threshold results in large solid or void regions, leading to sub-optimal structures. We find that this convergence issue relates to the topology of the stress tensor field that is simulated when applying the same external forces on the solid design domain. In particular, low convergence is observed in regions around so-called trisector degenerate points. Based on this observation, we propose an automatic initialization process that prescribes the topological skeleton of the stress field into the material field as solid simulation elements. These elements guide the material deposition around the degenerate points, but can also be remodelled or removed during the optimization. We demonstrate significantly improved convergence rates in a number of use cases with complex stress topologies. The improved convergence is demonstrated for infill optimization under homogeneous as well as spatially varying local volume constraints.

Associated publications

Stress Topology Analysis for Porous Infill Optimization
J Wang, J Wu and R Westermann
Structural and Multidisciplinary Optimization, 2022
[Paper] [BiB] [Demo Code]