Multigrid FEM Simulation using CUDA
Christian Dick, Joachim Georgii, Rüdiger Westermann
Computer Graphics and Visualization Group, Technische Universität München, Germany
Background
In this project we develop GPU-based numerical solvers for simulating elastic deformable objects in real time. Our techniques are based on finite element discretizations of the deformable objects using hexahedra. We use computationally efficient multigrid methods for the numerical solution of partial differential equations on such discretizations, and we consider the co-rotational formulation of strain to handle geometric non-linearities.
Due to the regular shape of the numerical stencil induced by the hexahedral regime, and since we use matrix-free formulations of all multigrid steps, computations and data layout can be restructured to avoid execution divergence and to support memory access patterns which enable the hardware to coalesce multiple memory accesses into single memory transactions. This enables to effectively exploit the GPU's parallel processing units and high memory bandwidth via the CUDA parallel programming API.
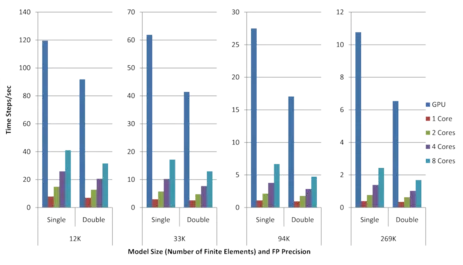
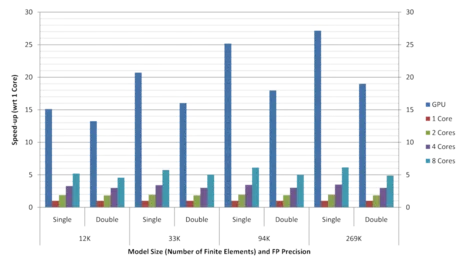
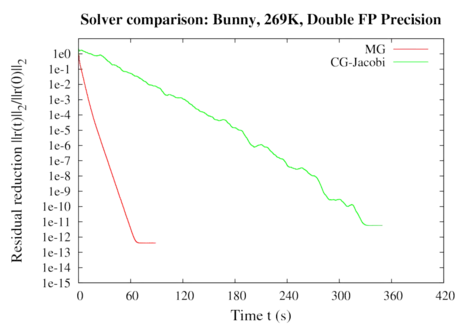
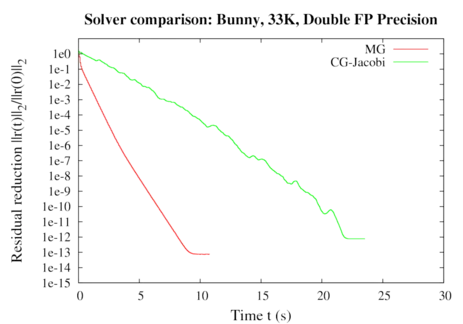
We demonstrate performance gains of up to a factor of 4 compared to our cache-aware CPU implementation running on 8 CPU cores. Even for complicated object boundaries, very good convergence rates of the numerical solver can be achieved (see graphs below). By using our approach, physics-based simulation at an object resolution of 64^3 is achieved at interactive rates. To the best of our knowledge, this is the first multigrid FEM approach for deformable body simulation using hexahedral elements that is running entirely on the GPU.
Publications
- A Real-Time Multigrid Finite Hexahedra Method for Elasticity Simulation using CUDA
C. Dick, J. Georgii, R. Westermann, Simulation Modelling Practice and Theory 19(2):801-816, 2011 [Bibtex] - A Real-Time Multigrid Finite Hexahedra Method for Elasticity Simulation using CUDA
C. Dick, J. Georgii, R. Westermann, Technical Report, July 2010 [Bibtex]
This technical report is a previous version of the paper. Note that the journal version contains updated timings for the NVIDIA Fermi GPU.
Deformable objects consisting of 30,000 (left) and 28,000 (right) hexahedral finite elements (112,000 and 98,000 DOF). The CUDA-based simulation runs entirely on the GPU at 69 and 74 time steps per second, respectively.
Time steps per second (left) and speed-ups (right) achieved on the Fermi GPU and on the CPU using 1, 2, 4, and 8 cores for models of different size as well as single and double floating point precision. Each time step includes the re-assembly of the system of equations due to the co-rotated strain formulation as well as two multigrid V-cycles, each with 2 pre- and 1 post-smoothing Gauss-Seidel steps. The speed-ups are measured with respect to 1 CPU core.
Convergence behavior of our multigrid solver (red curves) with respect to computing time (using 1 CPU core). For comparison, the convergence behavior of a conjugate gradient solver with Jacobi pre-conditioner (green curves) is included.