Visualizing the Stability of Critical Points in Uncertain Scalar Fields
Mihaela Mihai, Rüdiger Westermann
Computer Graphics and Visualization Group, Technische Universität München, Germany
Abstract
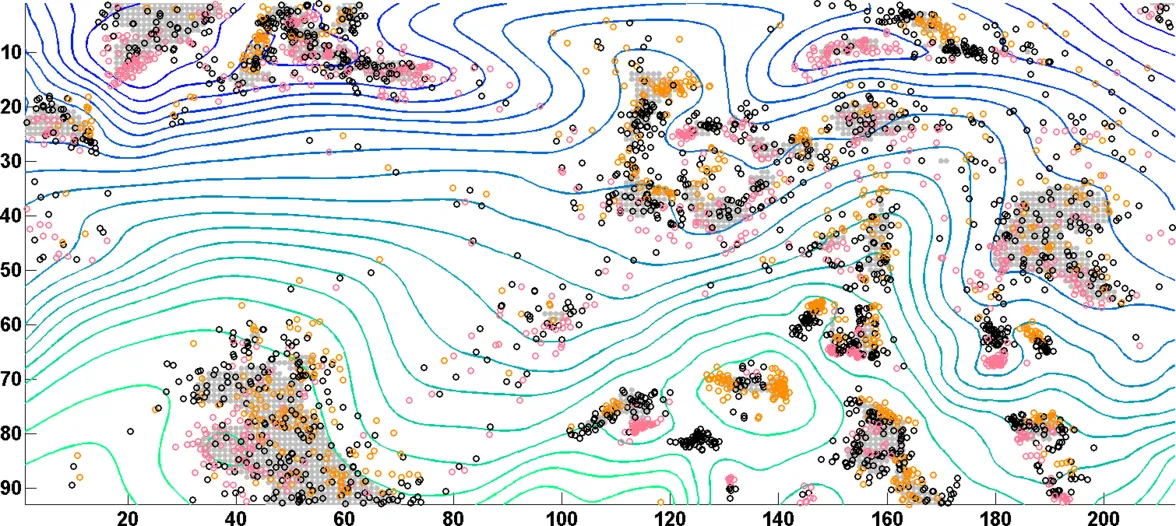
In scalar fields, critical points (points with vanishing derivatives) are important indicators of the topology of iso-contours. When the data values are affected by uncertainty, the locations and types of critical points vary and can no longer be predicted accurately. In this paper, we derive, from a given uncertain scalar ensemble, measures for the likelihood of the occurrence of critical points, with respect to both the positions and types of the critical points. In an ensemble, every instance is a possible occurrence of the phenomenon represented by the scalar values. We show that, by deriving confidence intervals for the gradient and the determinant and trace of the Hessian matrix in scalar ensembles, domain points can be classified according to whether a critical point can occur at a certain location and a specific type of critical point should be expected there. When the data uncertainty can be described stochastically via Gaussian distributed random variables, we show that even probabilistic measures for these events can be deduced.
Keywords: Uncertainty; Critical points; Stability; Scalar topology
Associated Publications
Mihaela Mihai, Rüdiger Westermann,
Visualizing the stability of critical points in uncertain scalar fields,
Computers & Graphics, Volume 41, June 2014, Pages 13-25, ISSN 0097-8493,
dx.doi.org/10.1016/j.cag.2014.01.007.
(http://www.sciencedirect.com/science/article/pii/S0097849314000247)